| ปริมาตรรูปทรงที่มีหน้าเป็นรูปหลายเหลี่ยม (polyhedron) รูปทรงเรขาคณิตที่มีผิวหน้าเป็นรูปหลายเหลี่ยม เช่น หีบเสื้อผ้า กล่องสี่เหลี่ยม ตู้เก็บกับข้าว มีผิวหน้าเป็นรูปสี่เหลี่ยมผืนผ้า หมอนขวาน มีผิวหน้าเป็นรูปสี่เหลี่ยมผืนผ้าสามรูป และหัวท้ายมีผิวหน้าเป็นรูปสามเหลี่ยม วิชาคณิตศาสตร์แบ่งรูปทรงนี้ ออกเป็นประเภทต่างๆ ดังนี้ | |
| |
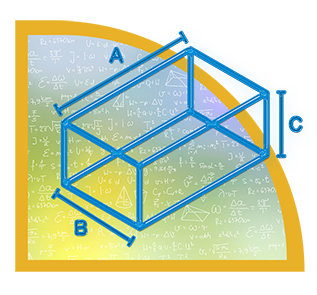
| ถ้าผิวด้านข้างของรูปปริซึมเป็นรูปสี่เหลี่ยมผืนผ้า และตั้งฉากกับฐานของปริซึมเราเรียกปริซึมชนิดนี้ว่า ปริซึมตรง ถ้าผิวด้านข้างไม่ตั้งฉากกับฐาน เราเรียกว่า ปริซึมเอียง กล่องสี่เหลี่ยมเป็นตัวอย่างของปริซึมตรงมีฐานเป็นรูปสี่เหลี่ยมผืนผ้า หมอนขวานเป็นตัวอย่างของปริซึมตรงมีฐานเป็นรูปสามเหลี่ยม ปริซึมที่มีผิวหน้าทั้งหกเป็นรูปสี่เหลี่ยมจัตุรัสเราเรียกว่า รูปลูกบาศก์ (cube) เช่น ลูกเต๋า เป็นต้น ปริมาตรของปริซึมตรง = พื้นที่ฐาน x ความสูง ถ้าปริซึมเอียงเราต้องหาความสูงซึ่งตั้งได้ฉากกับฐานของปริซึม จากวิชาเรขาคณิต เราทราบว่า ปริซึมสองรูปที่ตั้งอยู่บนฐาน ที่มีพื้นที่เท่ากัน และมีความสูงเท่ากันจะมีปริมาตรเท่ากัน ดังนั้นจึงได้สูตรการหาปริมาตรของปริซึมเท่ากับ พื้นที่ฐาน x ความสูง | |
1. รูปปริซึม2. รูปพีระมิด | |
| ถ้าลากเส้นตรงจากยอดของพีระมิดมาตั้งฉากกับฐาน เส้นตั้งฉากนี้ผ่านจุดศูนย์ถ่วงของฐานด้วย เราเรียกพีระมิดชนิดนี้ว่า พีระมิดตรง ปริมาตรของรูปพีระมิดตรง = 1/3 x พื้นที่ฐาน x ความสูง พีระมิดในประเทศอียิปต์เป็นพีระมิดที่มีฐานเป็นรูปสี่เหลี่ยม การก่อสร้างพีระมิดเหล่านี้นับเป็นความมหัศจรรย์ของมนุษยชาติทีเดียว รูปทรงที่มีผิวหน้าเป็นรูปหลายเหลี่ยมด้านเท่าเท่ากันทุกหน้า มีเพียง 5 แบบเท่านั้น ดังรูปต่อไปนี้ | |
| |
|
1. รูปเตตราเฮดรอน (tetrahedron)
2. รูปออคตาเฮดรอน (octahedron)
| |
|
3. รูปอิโคซาเฮดรอน (icosahedron)
4. รูปเหลี่ยมลูกบาศก์ (cube)
| 5. รูปโดเดคาเฮดรอน (dodecahedron) ลักษณะผิวหน้าเป็นรูปห้าเหลี่ยม มีผิวหน้า 12 หน้า จุดยอดมุม 20 มุม เส้นขอบ 30 เส้น |
| รูปทรงที่มีผิวหน้าเป็นรูปหลายเหลี่ยมด้านเท่าเท่ากันทุกหน้านั้น มีเพียง 5 ชนิดเท่านั้น รูปทรงอื่นๆ นั้นมีอีกมากมาย แต่จะไม่มีผิวหน้าเท่ากันเหมือนกันทุกหน้า รูปผลึกต่างๆ ในธรรมชาติล้วนมีลักษณะเป็นทรงรูปเหลี่ยม อัญมณีต่างๆ ที่ช่างได้เจียระไนแล้ว ก็ล้วนประดิษฐ์ให้เป็นรูปทรงเหลี่ยมทั้งนั้น การหาพื้นที่ผิวและปริมาตรของรูปทรงเหล่านี้ ก็อาจจะกระทำได้เช่นกัน | |
| จำนวนผิวหน้า จำนวนจุดยอดมุม และจำนวนเส้นขอบของรูปทรงที่มีหน้า เป็นรูปหลายเหลี่ยมนี้ มีความเกี่ยวข้องกัน ผู้ที่สังเกตเห็นความเกี่ยวข้องนี้ และ เขียนเป็นทฤษฎีคือ ออยเลอร์ ทฤษฎีของออยเลอร์กล่าวว่าถ้าให้ F, E และ V แทนจำนวนผิวหน้า จำนวนเส้นขอบ และจำนวนจุดยอดมุม ของรูปทรง ตามลำดับ จะได้ความสัมพันธ์ว่า E + 2 = F + V เช่น รูปปริซึมที่มีฐานเป็นรูปสี่เหลี่ยมจะมีผิวหน้า 6 หน้า จุดยอดมุม 8 มุม และ เส้นขอบ 12 เส้น ดังนั้น F = 6 V = 8 E = 12 จะเห็นได้ว่า 12 + 2 = 6 + 8 ทฤษฎีของออยเลอร์นี้ใช้ได้กับรูปทรงที่มีผิวหน้าเป็นรูปหลายเหลี่ยมทุกชนิด ดังนั้น ถ้าเราทราบค่า F, E และ V เพียงสองค่าเท่านั้น ก็จะหาค่าที่สามได้ทันที |
